pipe buckling equation
If a structure is subjected to a gradually increasing load when the load reaches a critical level a member may suddenly change shape and the structure and component is said to have. Buckling equations allow us to determine the critical loads that cause the loss of stability of thin-walled structures under compression or shear.
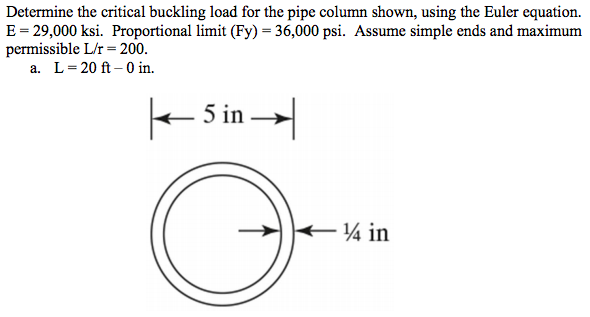
Solved Determine The Critical Buckling Load For The Pipe Chegg Com
The axial load is negative in compression.

. Knowing how much force is needed to buckle the pipe is essential. The buckling failure mode might imply that elastic buckling would occur with deflections that are beyond linear analysis limits. Than a shell-buckling problem.
The first step when determining buckling forces is to calculate the Column Slenderness Ratio Cc that divides elastic and inelastic buckling. For the unpressurized pipe the critical bending moment of local buckling can be calculated with Eq. 810 Buckling Equations.
Remember buckling is a bending failure rather than a failure due to direct compression crushing. 49 here as well as a buckling check in accordance with the external pressure design rules of ASME BPVC Section VIII Division 1. See the instructions within the documentation for more details on performing this analysis.
E Modulus of Elasticity approximately 3010 6 for steel. In Section 42 plastic buckling equations are derived. A buried pipe derives support against buckling from stable soil surround.
When an unstiffened short or intermediate lengths - thin-walled cylindrical shell is subjected to external hydrostatic pressure the tangential compressive tangential compressive stress reaches a critical value that the pipe is no longer able to maintain its initial circular shape the pipe failure is called elastic buckling failure. For values of E refer to ASNZS 25661. E modulus of elastisity lbin 2 Pa Nm 2 L length of column in m I Moment of inertia in 4 m 4.
At mid-length for the pinned. The bending deflection of pipe beam with uniform load is straight forward calculation with section modulus of pipe in tables. Flanges heads and stiffeners that comply with ASME.
Long columns can be analysed with the Euler column formula. In structural engineering buckling is the sudden change in shape of a structural component under load such as the bowing of a column under compression or the wrinkling of a plate under shear. 3a or 3b of ASME B313 the equation for internal pressure.
Where E is the soil modulus in MPa. This equation simply models the deflected shape of the column for a given flexural rigidity. M a_ 1 cdot D 2 cdot t cdot sigma_ text s cdot n a_ 2 2.
Our laterally deflected column behaves in much the same way as a beam. The buckling load is positive. The axial load is negative in compression.
2 2 d - d y CPy x ス1 where Cis an absolute elasticity and Pis the buckling load. The buckling load can be calculated using either the Euler equation suitable for long beams the Johnson equation suitable for short beams or the buckling load equation can be determined from the transition length. Columns fail by buckling when their critical load is reached.
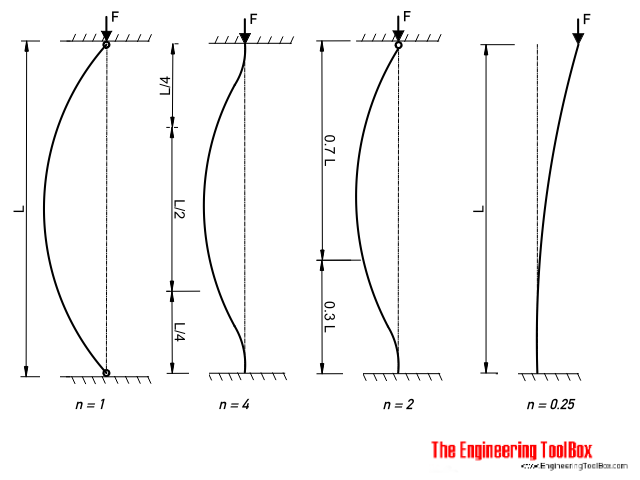
Buckling equations are based on the Euler static stability criterion according to which the critical load is the minimum the first reached load for which two equilibrium states of the structure can exist. Cosine is a periodic function and we know that cos x0 at intervals of pi2 3pi2 etc And so the above equation will equal zero when kL is equal to the following where n is an integer ranging from 1 to infinity. F allowable load lb N n factor accounting for the end conditions.
Before doing so it will buckle with the first mode which features a lower load. The Column Buckling calculator allows for buckling analysis of long and intermediate-length columns loaded in compression. R e ecr 2 where e is the eccentricity c is the centroidal distance and r is the radius of gyration.
Utilizes the SW Simulation buckling feature to determine the lowest buckling load. The buckling load is positive. The loading can be either central or eccentric.
1 where Fb buckling force lbf Fa axial force tension positive lbf pi internal pressure psi Ai ri2 where r i is the inside radius of the tubing in. Fixation on rod side eg. Thicker pipes used in deeper waters buckle and collapse in the plastic range.
The effective buckling pressure may be computed from. F n π 2 E I L 2 1 where. For beam buckling were interested in the second case ie.
Higher buckling modes feature larger buckling loads. Imperfections in a centrally loaded column are commonly approximated by using an eccentricity ratio of 025. H Burial depth to the top of pipe m Satisfaction of the buckling requirement is assured for normal pipe installations by the following equation γ wh w R wW c P v q a with vacuum γ wh w R wW c W L q a If live load is considered where γ w Specific weight of water kNm³ W c Vertical soil load kNm² P.
Buckling will generally occur about the axis with the lowest EI depending on. As a result the column cannot buckle according to a higher mode because it is unable to approach the required critical load. Buckling will generally occur about the axis with the lowest EI depending on.
For straight pipe under external pressure there is a membrane stress check in accordance with Eq. Right click on the Part nameÆStudy to open the Study panel. Buckling occurs if the buckling force Fb is greater than a threshold force Fp known as the Paslay buckling force.
Their relative simplicity makes them useful tools in design. Assign a new Study name select Buckling as the Type of analysis and use the thin shell as the Model type click OK. However if the lateral deflections are prevented at a point of the column eg.
As for P c P b should be multiplied by a temperatureloading time factor if required see table 311. As today a column buckling is calculated as with the formula by Euler in 1757 2 3 as shown below. Our task now is to.
P - Critical pressure of buckling on the external surface of the shell. The buckling load can be calculated using either the Euler equation suitable for long beams the Johnson equation suitable for short beams or the buckling load equation can be determined from the transition length. Youre likely to have come across this equation elsewhere in your engineering studies.
BASIC FORMULAS Critical pressure P. You might want to set some deflection limits to check your selection of pipe size. Practical factors that affect collapse include initial imperfections such as ovality and wall thickness variations.
The buckling force Fb is defined as. P 16Es2 LD 1 1-ν23 s2 025D2025 MATERIALS PROPERTIES OTHER CALCULATORS AREA MOMENTS OF INERTIA BEAM CALCULATORS TORSION OF BARS CIRCULAR FLAT PLATES BUCKLING ELASTIC CONTACT IMPACT LOADS NATURAL. 2 in which the hardening exponent is taken into consideration.
See the reference section for details on the equations used. According to Gere values of eccentricity ratio are most commonly less than 1 but typical values are between 0 to 3. From the formula above another formula to figure out a limit load was easily induced.
1114Cc π2E Yp.
Buckling Of Columns Euler Tetmajer Calculator Formulas Di Strommer

Mechanical Engineering Calculators Mechanical Engineering Maths Solutions Physics Lessons

Mechanical Engineering Calculators Mechanical Engineering Maths Solutions Physics Mechanics

Euler Buckling Load Calculation Example 2 Mechanics Of Materials Youtube
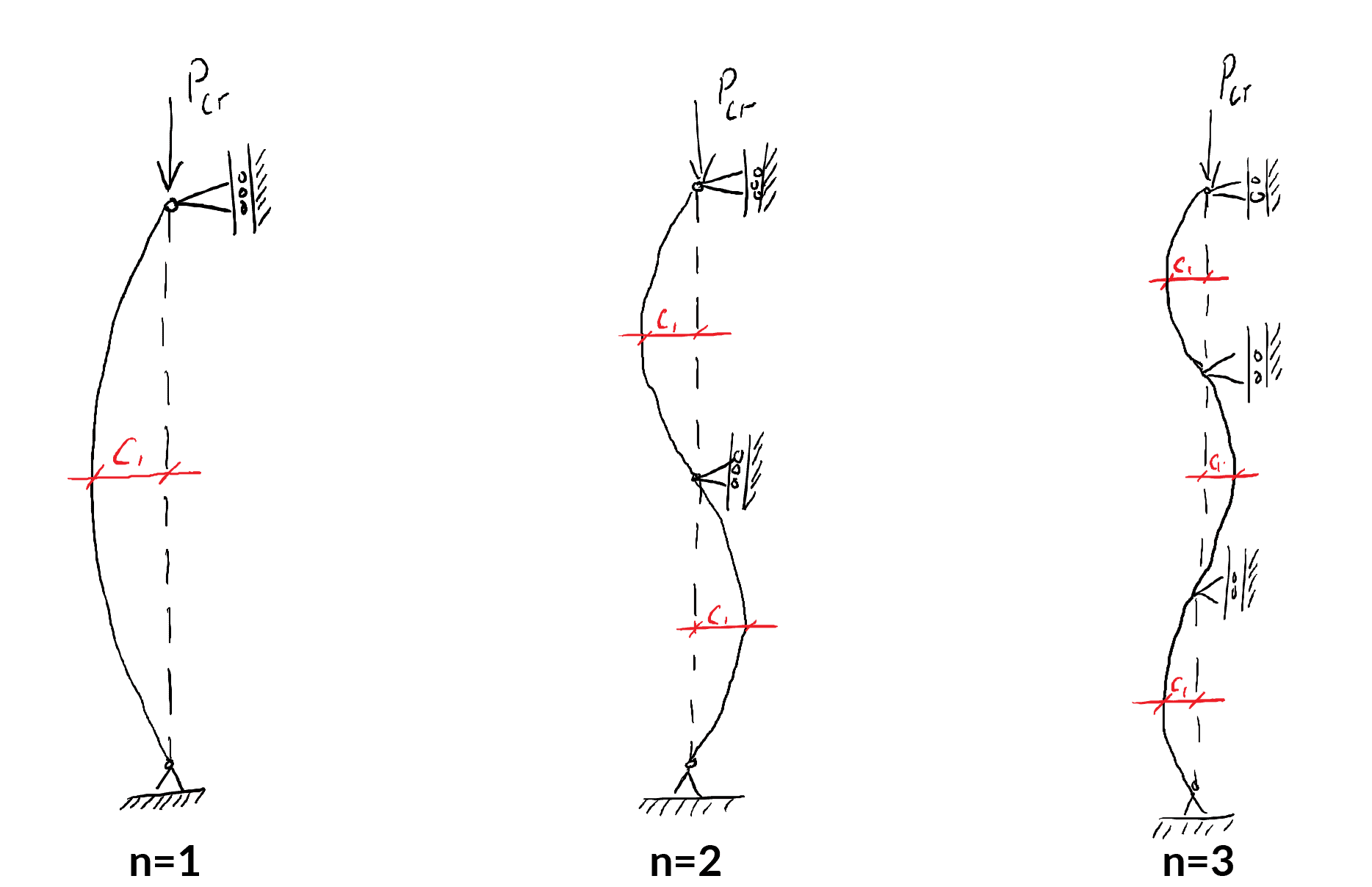
Column Buckling Equations And Buckling Behaviour Degreetutors Com

Buckling Analysis Or Structural Instability Is The Study Of Phenomena That Can Lead To Collapse Of The Civil Engineering Design Engineering Structural Analysis

Mechanical Engineering Calculators Mechanical Engineering Physics Lessons Mathematics Education Teaching
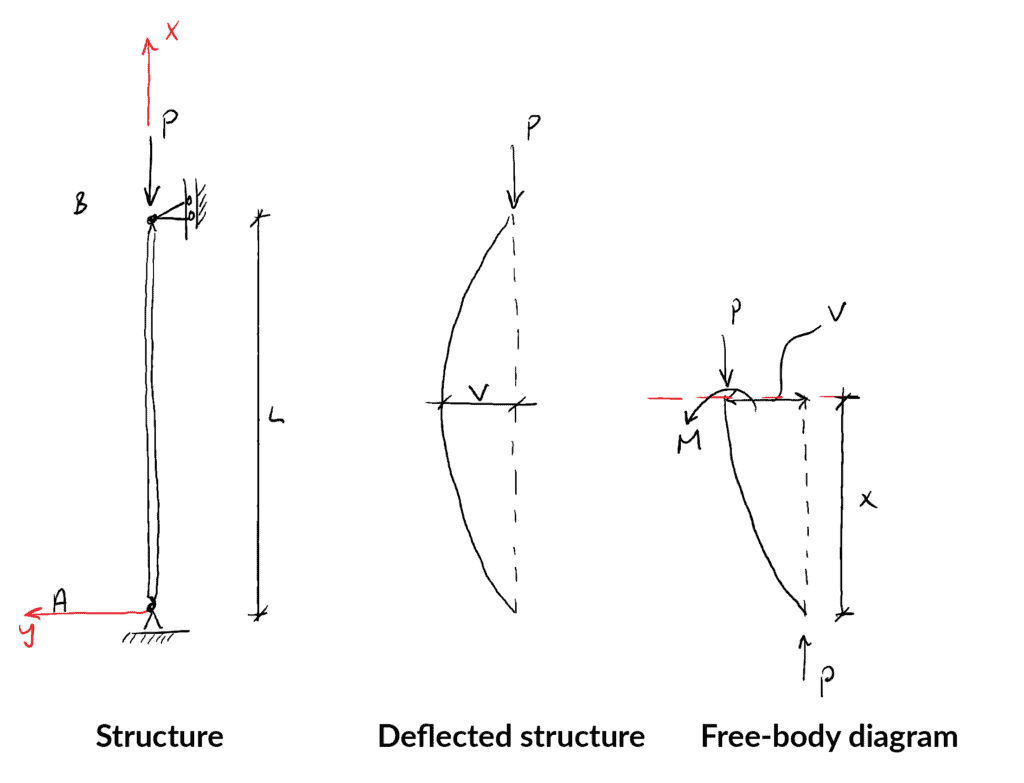
Column Buckling Equations And Buckling Behaviour Degreetutors Com

Euler Buckling An Overview Sciencedirect Topics
Buckling Of Columns Euler Tetmajer Calculator Formulas Di Strommer






Comments
Post a Comment